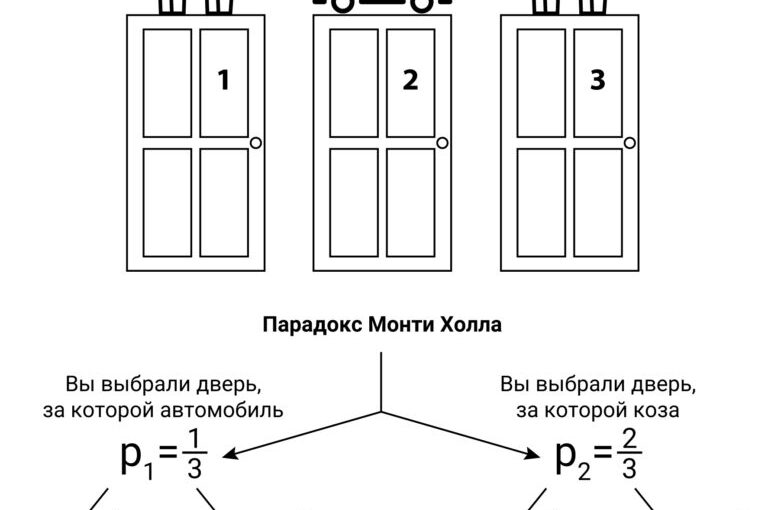
Парадокс Монти Холла — это задача теории вероятностей, основанная на сюжете американского игрового шоу Let’s Make a Deal. Её суть заключается в следующем:
Условия задачи
— перед участником 3 двери: за одной — автомобиль, за двумя другими — козы;
— участник выбирает одну дверь (например, Дверь 1);
— ведущий, знающий, где автомобиль, открывает одну из оставшихся дверей, за которой точно находится коза (например, Дверь 3).
Участнику предлагают выбор: остаться при своём выборе (Дверь 1) или переключиться на оставшуюся закрытую дверь (Дверь 2).
Парадокс
Интуитивно кажется, что шансы выиграть автомобиль после открытия одной двери становятся 50/50. Однако математически выгоднее переключиться — вероятность победы при этом составляет 2/3, а не 1/2.
Почему так происходит
— изначальный выбор: вероятность выбрать автомобиль — 1/3, козу — 2/3;
— действие ведущего: он всегда открывает дверь с козой, что меняет информацию о системе:
— если участник изначально выбрал козу (вероятность 2/3), то после открытия ведущим второй «козьей» двери, автомобиль гарантированно находится за оставшейся;
— если участник изначально выбрал автомобиль (вероятность 1/3), переключение приведёт к проигрышу.
Наглядный пример
Автомобиль за Дверью 1:
— выбор участника: Дверь 1 → ведущий откроет Дверь 2 или 3 → переключение = проигрыш;
— выбор участника: Дверь 2 → ведущий откроет Дверь 3 → переключение на Дверь 1 = выигрыш;
— выбор участника: Дверь 3 → ведущий откроет Дверь 2 → переключение на Дверь 1 = выигрыш.
В двух случаях из трёх переключение даёт победу (2/3).
Почему это парадокс
Задача противоречит интуиции, так как кажется, что после исключения одной двери шансы должны уравняться. Однако ключевым фактором является поведение ведущего — он не действует случайно, а использует знание о расположении автомобиля, что меняет вероятности.
Заключение
Парадокс Монти Холла демонстрирует важность учёта условных вероятностей и контекста в задачах принятия решений. Математически оптимальная стратегия — всегда переключаться.